Selection Sort
Selection sort is a simple sorting algorithm that works by repeatedly finding the minimum element from the unsorted portion and placing it at the beginning. It divides the array into a sorted portion (initially empty) and an unsorted portion (initially the entire array).
Properties
Section titled “Properties”- Comparison-based: Works by comparing elements to find minimum
- In-place sorting: Sorts the array without using extra space
- Unstable algorithm: Does not maintain relative order of equal elements
- Simple implementation: Easy to understand and implement
How it Works
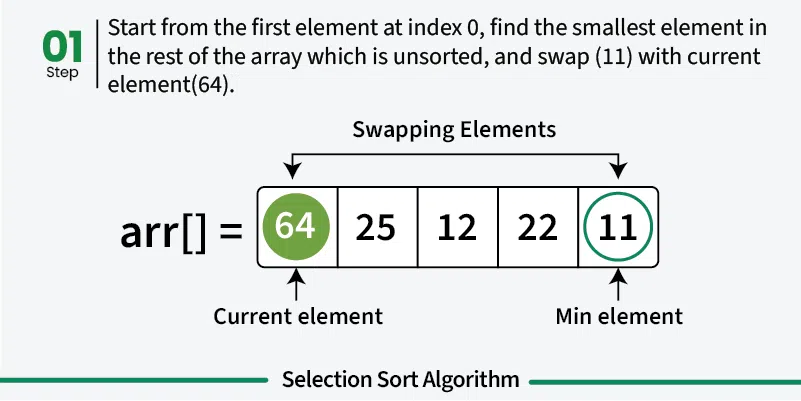
Section titled “How it Works”- Start with first position: Assume first element is the minimum
- Find minimum in unsorted portion: Scan through unsorted part to find the actual minimum
- Swap with first position: Replace the first element with the found minimum
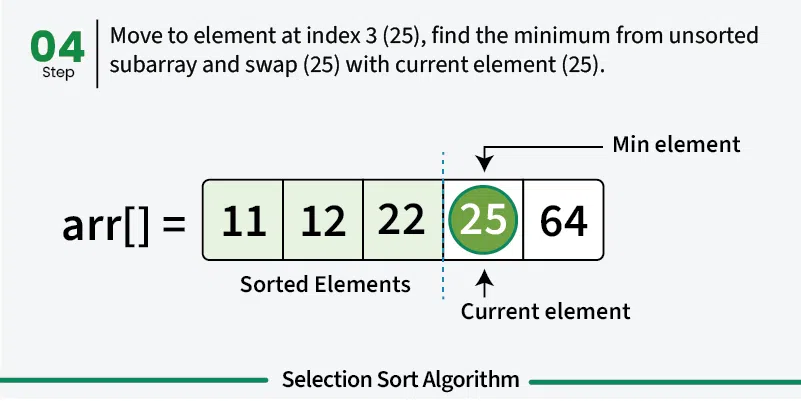
- Move to next position: The first element is now sorted, move to second position
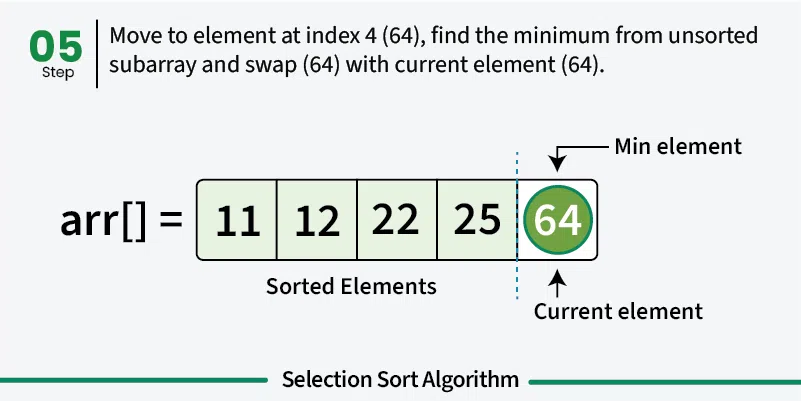
- Repeat: Find minimum in remaining unsorted portion and swap with current position
- Continue: Repeat until all elements are in their correct positions
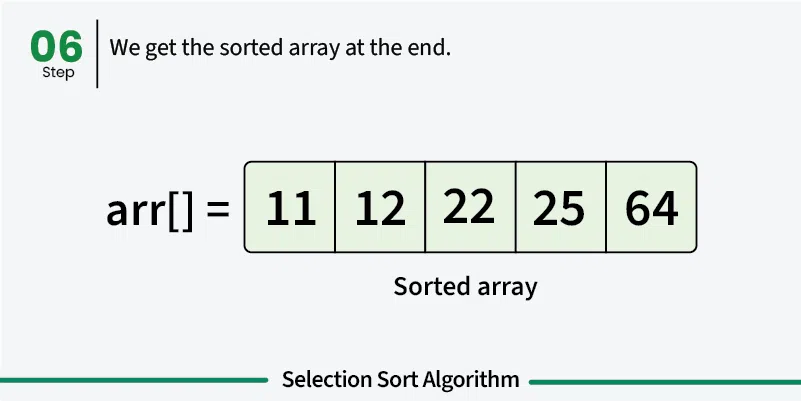
- Done: Array is fully sorted when all positions are filled


Use Cases
Section titled “Use Cases”- Educational purposes: Good for learning sorting concepts
- Small datasets: Acceptable for very small arrays
- Memory-constrained environments: Uses minimal extra memory
- When simplicity matters: When implementation simplicity is priority
Time Complexity
Section titled “Time Complexity”- Best case: O(n²) - Even when array is already sorted
- Average case: O(n²) - Random order of elements
- Worst case: O(n²) - When array is reverse sorted
Note: Unlike bubble sort, selection sort always performs O(n²) comparisons regardless of input.
Space Complexity
Section titled “Space Complexity”- O(1): Constant space, only uses a few variables
Advantages
Section titled “Advantages”- Simple to understand: Intuitive algorithm concept
- In-place sorting: Minimal memory requirements
- Consistent performance: Always O(n²), predictable behavior
- Minimum number of swaps: Makes at most n-1 swaps
Disadvantages
Section titled “Disadvantages”- Poor performance: O(n²) time complexity for all cases
- Not adaptive: Doesn’t improve performance for partially sorted arrays
- Unstable: May change relative order of equal elements
- Not suitable for large datasets: Inefficient for large arrays
Example
Section titled “Example”public class SelectionSort { // Selection sort implementation public static void selectionSort(int[] array) {
// 📌 Part 1: Traverse through all array elements for (int i = 0; i < array.length - 1; i++) {
// 📌 Part 2: Find the minimum element in remaining unsorted array int minIndex = i;
// 📌 Part 3: Scan through unsorted portion for (int j = i + 1; j < array.length; j++) {
// 📌 Part 4: Update minIndex if current element is smaller if (array[j] < array[minIndex]) { minIndex = j; }
}
// 📌 Part 5: Swap the found minimum element with the first element if (minIndex != i) { int temp = array[minIndex]; array[minIndex] = array[i]; array[i] = temp; }
}
}
public static void main(String[] args) { int[] numbers = {64, 34, 25, 12, 22, 11, 90};
System.out.print("Original: "); for (int num : numbers) { System.out.print(num + " "); }
selectionSort(numbers); System.out.println();
System.out.print("Sorted: "); for (int num : numbers) { System.out.print(num + " "); } }}