Trees

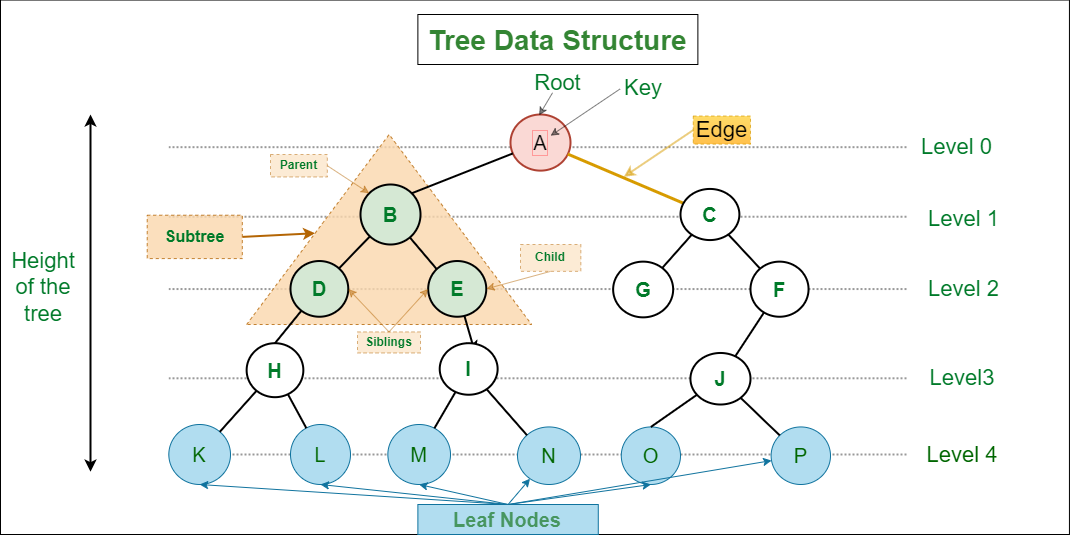
A tree is a hierarchical data structure consisting of nodes connected by edges. It resembles an upside-down tree with a root at the top and branches extending downward. Each node can have multiple children, but only one parent (except the root node which has no parent).

Properties

• Hierarchical structure with parent-child relationships: Nodes are organized in levels with clear parent-child connections.
• One root node (no parent): The top-most node that serves as the starting point of the tree.
• Each node can have multiple children: Nodes can branch out to any number of child nodes.
• N nodes have N-1 edges: A tree with N nodes always has exactly N-1 connecting edges.

Use Cases

• File systems: Representing folder and file hierarchies in operating systems.

Types

• Binary Tree: Each node has at most 2 children

Operations

• Search: Find a specific value in the tree.
• Insertion: Add a new node to the tree.
• Deletion: Remove a node from the tree.
• Traversal: Visit all nodes in a specific order (Inorder, Preorder, Postorder).

Traversal Methods

• Inorder: Left → Root → Right
• Preorder: Root → Left → Right
• Postorder: Left → Right → Root
• Level order: Breadth-first traversal

Advantages

• Efficient searching and sorting: Balanced trees provide logarithmic time complexity for common operations.
• Hierarchical data representation: Natural way to represent data with parent-child relationships.
• Dynamic size: Can grow and shrink as needed during runtime.
• Various traversal methods: Multiple ways to visit and process nodes.

Disadvantages

• No constant time operations: Most operations require traversing the tree structure.
• Complex implementation: More complex to implement compared to linear data structures.
• Recursive nature: Many tree algorithms are recursive, which can cause stack overflow for very deep trees.

Example

// Simple binary tree node class
class TreeNode {
  int data;
  TreeNode left;
  TreeNode right;

  TreeNode(int value) {
    this.data = value;
    this.left = null;
    this.right = null;
  }
}

// Creating a binary tree
TreeNode root = new TreeNode(1);       // Root node
root.left = new TreeNode(2);           // Left child of root
root.right = new TreeNode(3);          // Right child of root
root.left.left = new TreeNode(4);      // Left child of node 2
root.left.right = new TreeNode(5);     // Right child of node 2

// Tree structure:
//       1
//      / \
//     2   3
//    / \
//   4   5

// Inorder traversal (Left -> Root -> Right)
public void inorderTraversal(TreeNode node) {
  if (node != null) {
    inorderTraversal(node.left);    // Visit left subtree
    System.out.print(node.data + " "); // Visit root
    inorderTraversal(node.right);   // Visit right subtree
  }
}

// Usage: inorderTraversal(root); // Output: 4 2 5 1 3