Graphs
This content is for DSA. Switch to the latest version for up-to-date documentation.
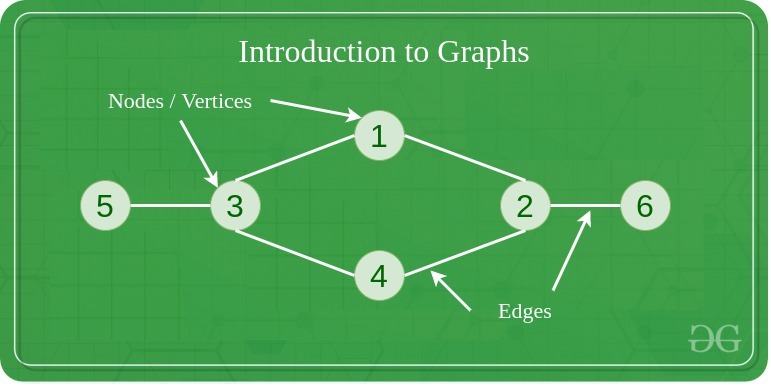
A graph is a non-linear data structure consisting of vertices (nodes) connected by edges (links). Unlike trees, graphs can have cycles and multiple paths between nodes. Think of it like a network of cities connected by roads, where you can travel between cities through various routes.
Properties
Section titled “Properties”- Set of vertices (nodes) and edges (connections): The fundamental components that make up a graph structure.
- Can be directed or undirected: Edges may have direction (one-way) or be bidirectional (two-way).
- Can be weighted or unweighted: Edges may have associated costs or values, or all be considered equal.
- Can be cyclic or acyclic: May contain loops that return to the starting vertex or be cycle-free.
- Can be connected or disconnected: All vertices may be reachable from each other, or exist in separate components.
Use Cases
Section titled “Use Cases”- Social networks: Representing relationships between people (friends, followers, connections).
- Transportation networks: Modeling roads, flight routes, and public transit systems.
- Computer networks: Representing connections between computers, routers, and servers.
- Dependency graphs: Showing dependencies between tasks, modules, or packages.
- Game maps and pathfinding: Creating navigable game worlds and finding optimal routes.
- Web page linking: Representing hyperlinks between web pages for search engines.
- Directed Graph: Edges have direction
- Undirected Graph: Edges have no direction
- Weighted Graph: Edges have weights/costs
- Unweighted Graph: All edges have same weight
- Complete Graph: Every vertex connected to every other vertex
- Bipartite Graph: Vertices can be divided into two disjoint sets
Representations
Section titled “Representations”- Adjacency Matrix: 2D array of connections
- Adjacency List: List of neighbors for each vertex
- Edge List: List of all edges
Operations
Section titled “Operations”- Add Vertex: O(1) in adjacency list - Add a new node to the graph.
- Add Edge: O(1) in adjacency list - Create a connection between two vertices.
- Remove Vertex: O(V + E) where V = vertices, E = edges - Delete a node and all its connections.
- Remove Edge: O(V) in adjacency list - Remove a connection between two vertices.
- Find Edge: O(V) in adjacency list, O(1) in adjacency matrix - Check if two vertices are connected.
Traversal Algorithms
Section titled “Traversal Algorithms”- Depth-First Search (DFS): Uses stack/recursion
- Breadth-First Search (BFS): Uses queue
- Both have O(V + E) time complexity
Advantages
Section titled “Advantages”- Models complex relationships: Can represent any type of connection between entities.
- Flexible structure: Supports various types of connections and relationships.
- Many algorithms available: Rich set of algorithms for traversal, shortest path, and analysis.
- Real-world problem modeling: Natural representation for many practical problems.
- Powerful analysis capabilities: Can analyze connectivity, centrality, and network properties.
Disadvantages
Section titled “Disadvantages”- Complex implementation: More complicated to implement compared to linear data structures.
- High memory usage for dense graphs: Adjacency matrices use O(V²) space regardless of edge count.
- Some operations can be expensive: Operations like finding shortest paths can be computationally intensive.
- No guaranteed ordering: Unlike trees, graphs don’t have a natural hierarchical structure.
- Potential for infinite loops: Cycles in graphs can cause algorithms to run indefinitely without proper handling.
Example
Section titled “Example”import java.util.*;
// Graph implementation using adjacency listclass Graph { private Map<Integer, List<Integer>> adjacencyList;
public Graph() { adjacencyList = new HashMap<>(); }
// Add a vertex to the graph public void addVertex(int vertex) { adjacencyList.putIfAbsent(vertex, new ArrayList<>()); }
// Add an edge between two vertices (undirected) public void addEdge(int source, int destination) { adjacencyList.get(source).add(destination); adjacencyList.get(destination).add(source); // For undirected graph }
// Display the graph public void displayGraph() { for (int vertex : adjacencyList.keySet()) { System.out.println(vertex + " -> " + adjacencyList.get(vertex)); } }}
// Usage exampleGraph graph = new Graph();
// Add verticesgraph.addVertex(1);graph.addVertex(2);graph.addVertex(3);graph.addVertex(4);
// Add edges (connections)graph.addEdge(1, 2); // Connect 1 to 2graph.addEdge(1, 3); // Connect 1 to 3graph.addEdge(2, 4); // Connect 2 to 4graph.addEdge(3, 4); // Connect 3 to 4
// Display the graphgraph.displayGraph();// Output:// 1 -> [2, 3]// 2 -> [1, 4]// 3 -> [1, 4]// 4 -> [2, 3]