Insertion Sort

Insertion sort is a simple sorting algorithm that builds the final sorted array one element at a time. It works by taking elements from the unsorted portion and inserting them into their correct position in the sorted portion, similar to how you might sort playing cards in your hand.

Play

Properties

• Comparison-based: Works by comparing elements to find correct position
• In-place sorting: Sorts the array without using extra space
• Stable algorithm: Maintains relative order of equal elements
• Adaptive: Performs better on partially sorted arrays

How it Works

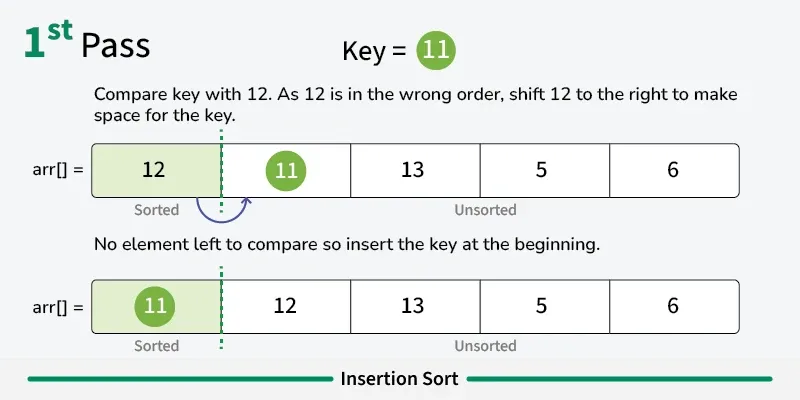
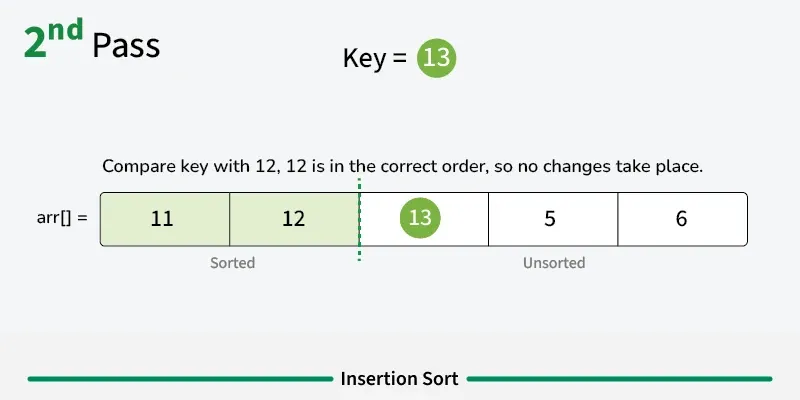
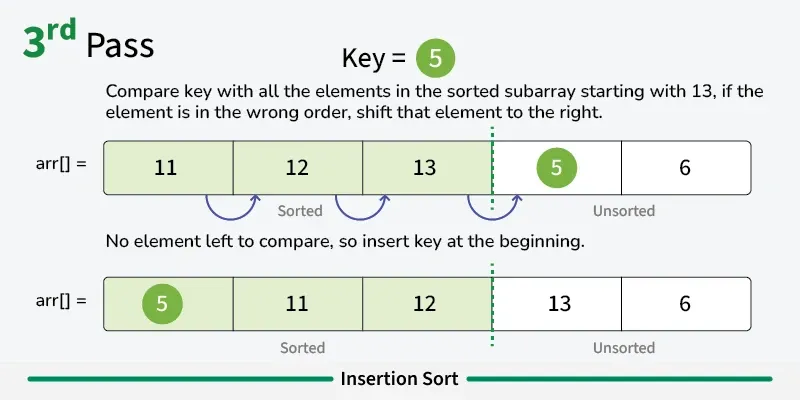
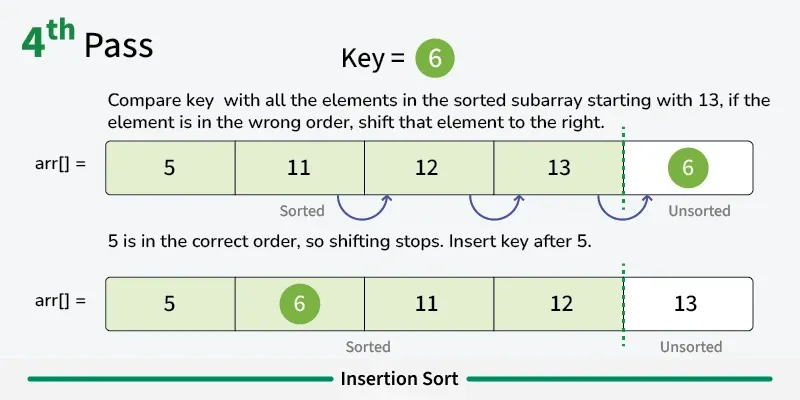
1. Start with second element: Assume first element is already “sorted”
2. Pick current element: Take the next element from unsorted portion
3. Compare with sorted elements: Compare with elements in sorted portion (from right to left)
4. Shift elements: Move larger elements one position to the right
5. Insert in correct position: Place current element in its correct position
6. Expand sorted portion: The sorted portion now includes the inserted element
7. Repeat: Continue with next element until all elements are processed
8. Done: Array is fully sorted

Use Cases

• Small datasets: Efficient for small arrays (typically < 50 elements)
• Nearly sorted data: Performs excellently on already sorted or nearly sorted data
• Online algorithm: Can sort data as it’s received
• Hybrid sorting algorithms: Used as a subroutine in advanced algorithms like Quicksort

Time Complexity

• Best case: O(n) - When array is already sorted
• Average case: O(n²) - Random order of elements
• Worst case: O(n²) - When array is reverse sorted

Space Complexity

• O(1): Constant space, only uses a few variables

Advantages

• Simple implementation: Easy to understand and code
• Efficient for small datasets: Better than other O(n²) algorithms for small arrays
• Adaptive: Performance improves with partially sorted data
• Stable: Maintains relative order of equal elements
• In-place: Requires only constant extra memory
• Online: Can process elements as they arrive

Disadvantages

• Poor performance on large datasets: O(n²) time complexity is inefficient for large arrays
• More comparisons than selection sort: Generally performs more comparisons
• Not suitable for large-scale applications: Better algorithms exist for large datasets

Example

public class InsertionSort {
  // Basic insertion sort implementation
  public static void insertionSort(int[] array) {

    // 📌 Part 1: Start from second element (index 1) since first element is considered sorted
    for (int i = 1; i < array.length; i++) {

      // 📌 Part 2: Keep track of current element and last sorted position
      int currentElement = array[i]; // Element to be inserted
      int j = i - 1; // Index of last element in sorted portion

      // 📌 Part 3: Shift elements that are greater than currentElement to one position ahead
      while (j >= 0 && array[j] > currentElement) {
        array[j + 1] = array[j]; // Shift element to right
        j--;
      }

      // 📌 Part 4: Insert currentElement at its correct position
      array[j + 1] = currentElement;

    }

  }

  public static void main(String[] args) {
    int[] numbers = {64, 34, 25, 12, 22, 11, 90};

    System.out.print("Original: ");
    for (int num : numbers) {
      System.out.print(num + " ");
    }

    insertionSort(numbers);
    System.out.println();

    System.out.print("Sorted: ");
    for (int num : numbers) {
      System.out.print(num + " ");
    }
  }
}

Visualization