Bubble Sort

Bubble sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The process is repeated until the list is sorted. It’s called “bubble” sort because larger elements “bubble” to the top of the list.

Play

Properties

• Comparison-based: Works by comparing adjacent elements
• In-place sorting: Sorts the array without using extra space
• Stable algorithm: Maintains relative order of equal elements
• Simple implementation: Easy to understand and implement

How it Works

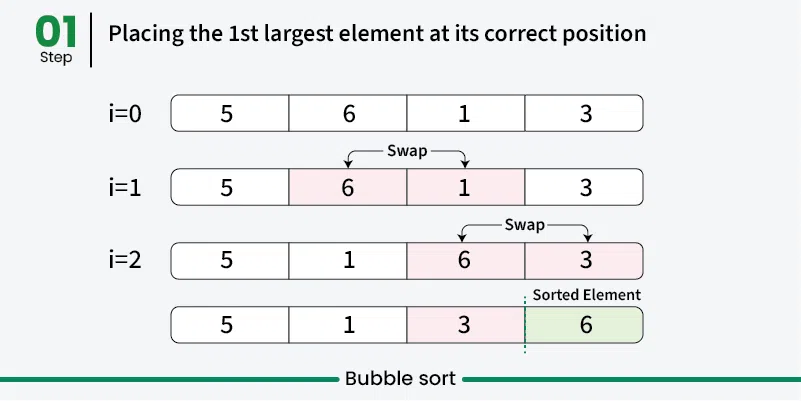
1. Start from beginning: Begin with the first element of the array
2. Compare adjacent elements: Compare current element with the next element
3. Swap if needed: If current element is greater than next, swap them
4. Move to next pair: Continue comparing adjacent pairs through the array
5. Complete one pass: After one complete pass, the largest element is in its correct position
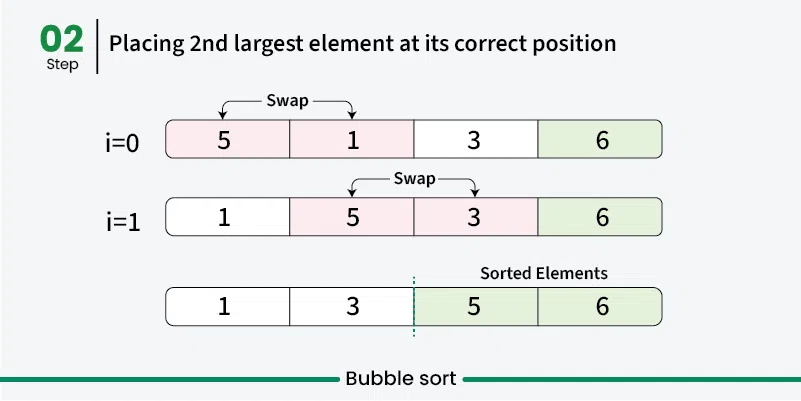
6. Repeat: Repeat the process for remaining unsorted elements
7. Optimization: In each pass, ignore the last sorted elements
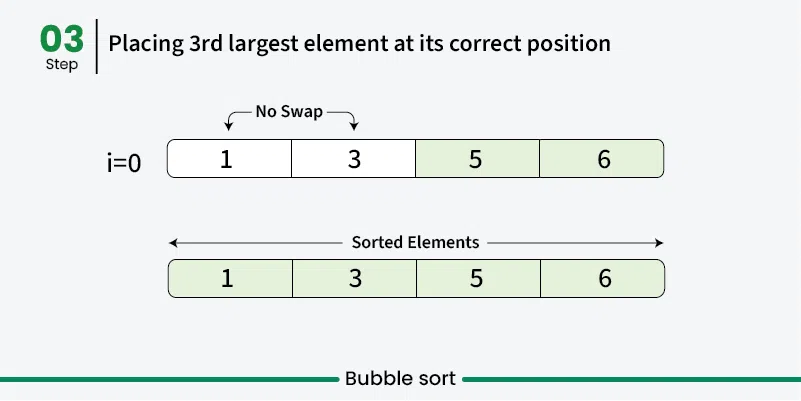
8. Done: Continue until no swaps are needed

Use Cases

• Educational purposes: Great for learning sorting concepts
• Small datasets: Acceptable performance for very small arrays
• Nearly sorted data: Performs better when data is already mostly sorted
• Simple implementation needed: When code simplicity is more important than efficiency

Time Complexity

• Best case: O(n) - When array is already sorted (with optimization)
• Average case: O(n²) - Random order of elements
• Worst case: O(n²) - When array is reverse sorted

Space Complexity

• O(1): Constant space, only uses a few variables for swapping

Advantages

• Simple to understand: Very intuitive algorithm
• In-place sorting: Doesn’t require additional memory
• Stable: Maintains relative order of equal elements
• Adaptive: Can be optimized to detect if array is already sorted

Disadvantages

• Poor performance: O(n²) time complexity makes it inefficient for large datasets
• Too many comparisons: Even for small improvements, requires many comparisons
• Not practical: Rarely used in real-world applications due to poor performance

Example

public class BubbleSort {
  // Bubble sort (stops early if array becomes sorted)
  public static void bubbleSort(int[] array) {
    boolean swapped;

    // 📌 Part 1: Outer loop for number of passes
    for (int i = 0; i < array.length - 1; i++) {
      swapped = false;

      // 📌 Part 2: Inner loop for comparing adjacent elements
      // Reduce the range in each pass since largest elements bubble up
      for (int j = 0; j < array.length - i - 1; j++) {

        // 📌 Part 3: Compare adjacent elements
        if (array[j] > array[j + 1]) {

          // 📌 Part 4: Swap elements
          int temp = array[j];
          array[j] = array[j + 1];
          array[j + 1] = temp;

          // Mark that a swap occurred
          swapped = true;

        }

      }

      // If no swapping occurred, array is sorted
      if (!swapped) {
        break;
      }

    }

  }

  public static void main(String[] args) {
    int[] numbers = {64, 34, 25, 12, 22, 11, 90};

    System.out.print("Original: ");
    for (int num : numbers) {
      System.out.print(num + " ");
    }

    bubbleSort(numbers);
    System.out.println();

    System.out.print("Sorted: ");
    for (int num : numbers) {
      System.out.print(num + " ");
    }
  }
}

Visualization