Binary Search
This content is for DSA. Switch to the latest version for up-to-date documentation.
Binary search is an efficient searching algorithm that works on sorted arrays by repeatedly dividing the search interval in half. It compares the target value with the middle element and eliminates half of the remaining elements in each step.
Properties
Section titled “Properties”- Requires sorted data: Only works on sorted arrays or lists
- Divide and conquer: Uses divide and conquer strategy
- Logarithmic time complexity: Much faster than linear search for large datasets
- Iterative or recursive: Can be implemented both ways
How it Works
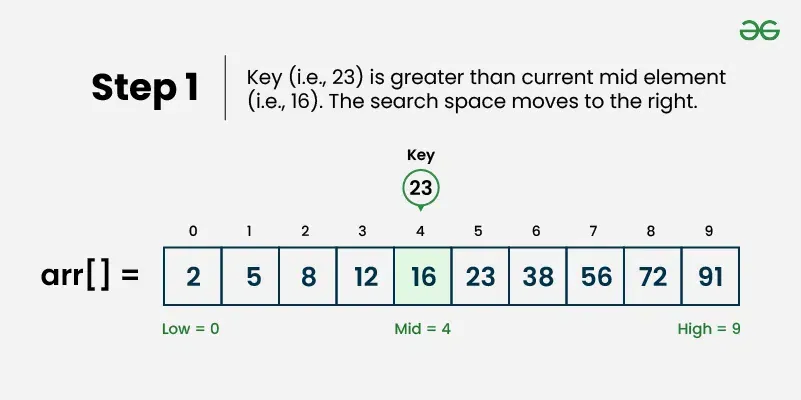
Section titled “How it Works”- Set boundaries: Define left (start) and right (end) pointers
- Find middle: Calculate middle index:
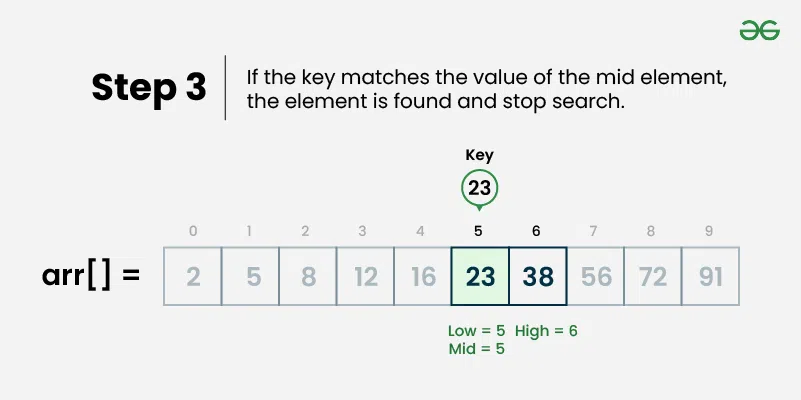
middle = (left + right) / 2 - Compare: Check if middle element equals target value
- Found: If equal, return the middle index
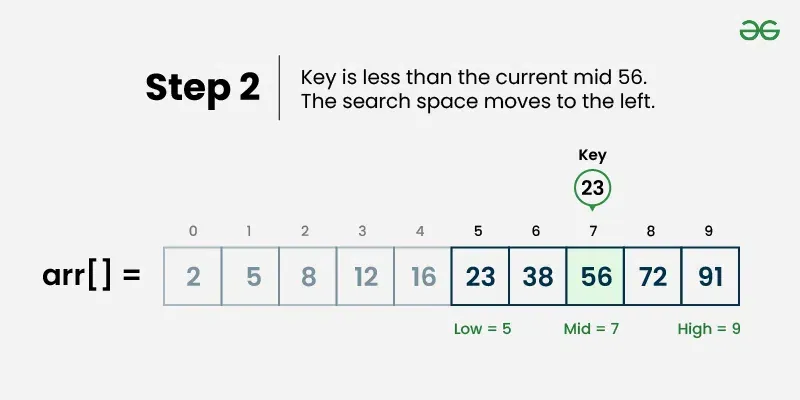
- Go left: If target is smaller, search left half (set right = middle - 1)
- Go right: If target is larger, search right half (set left = middle + 1)
- Repeat: Continue until element is found or left > right
- Not found: If left > right, element doesn’t exist in array

Use Cases
Section titled “Use Cases”- Large sorted datasets: When you have large amounts of sorted data
- Database indexing: Used in database systems for fast record retrieval
- Dictionary lookups: Finding words in sorted dictionaries
- Library systems: Searching books by ISBN or catalog numbers
Time Complexity
Section titled “Time Complexity”- Best case: O(1) - Element found at middle position
- Average case: O(log n) - Element found after several divisions
- Worst case: O(log n) - Element not found or at the edges
Space Complexity
Section titled “Space Complexity”- Iterative: O(1) - Constant space
- Recursive: O(log n) - Due to recursion stack
Advantages
Section titled “Advantages”- Very efficient: O(log n) time complexity is much faster than O(n)
- Predictable performance: Logarithmic time even in worst case
- Memory efficient: Iterative version uses constant space
- Simple concept: Easy to understand the divide-and-conquer approach
Disadvantages
Section titled “Disadvantages”- Requires sorted data: Array must be sorted beforehand
- Not suitable for small datasets: Overhead might not be worth it for small arrays
- Static data: Frequent insertions/deletions can make maintaining sorted order expensive
Example
Section titled “Example”public class BinarySearch { // Iterative binary search method public static int binarySearch(int[] array, int target) {
// 📌 Part 1: Initialize left and right pointers int left = 0; int right = array.length - 1;
// 📌 Part 2: Loop until left pointer exceeds right pointer while (left <= right) {
// 📌 Part 3: Calculate middle index int middle = left + (right - left) / 2;
// 📌 Part 4: Check if target is at middle if (target == array[middle]) { return middle; }
// 📌 Part 5: If target is smaller, search left half if (target < array[middle]) { right = middle - 1; } // 📌 Part 6: If target is larger, search right half else { left = middle + 1; }
}
return -1; // Element not found }
public static void main(String[] args) { int[] sortedNumbers = {11, 12, 22, 25, 34, 64, 90}; // Must be sorted! int target = 64;
System.out.println("Sorted Array: [11, 12, 22, 25, 34, 64, 90]"); System.out.println("Target: " + target);
// Using iterative approach int result = binarySearch(sortedNumbers, target); if (result != -1) { System.out.println("Element found at index: " + result); } else { System.out.println("Element not found"); } }}